Functional derivative
In mathematics and theoretical physics, the functional derivative is a generalization of the gradient. While the latter differentiates with respect to a vector with discrete components, the former differentiates with respect to a continuous function. Both of these can be viewed as extensions of the simple one-dimensional derivative in usual calculus. The mathematically formal treatment is the subject of functional analysis.
Contents |
Definition
Given a manifold M representing (continuous/smooth/with certain boundary conditions/etc.) functions φ and a functional F defined as
-
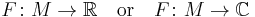 ,
,
the functional derivative of F, denoted 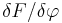 , is a distribution such that for all test functions f
, is a distribution such that for all test functions f
Using the first variation of  ,
, 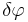 , in place of
, in place of  yields the first variation of
yields the first variation of  ,
, 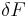 ; this is similar to how the differential is obtained from the gradient. Using a function
; this is similar to how the differential is obtained from the gradient. Using a function  with unit norm yields the directional derivative along that function.
with unit norm yields the directional derivative along that function.
In physics, it's common to use the Dirac delta function 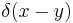 in place of a generic test function
in place of a generic test function  , for yielding the functional derivative at the point
, for yielding the functional derivative at the point  (this is a point of the whole functional derivative as a partial derivative is a component of the gradient):
(this is a point of the whole functional derivative as a partial derivative is a component of the gradient):
This works in cases when ![F[\varphi(x)%2B\varepsilon f(x)]](/2012-wikipedia_en_all_nopic_01_2012/I/cfd07ddbfaf66b69e7ed9fd6a3c174ae.png) formally can be expanded as a series (or at least up to first order) in
formally can be expanded as a series (or at least up to first order) in 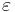 . The formula is however not mathematically rigorous, since
. The formula is however not mathematically rigorous, since ![F[\varphi(x)%2B\varepsilon\delta(x-y)]](/2012-wikipedia_en_all_nopic_01_2012/I/6eb6410c4c091e7c244f7d3482c7bb13.png) is usually not even defined.
is usually not even defined.
Formal description
The definition of a functional derivative may be made more mathematically precise and formal by defining the space of functions more carefully. For example, when the space of functions is a Banach space, the functional derivative becomes known as the Fréchet derivative, while one uses the Gâteaux derivative on more general locally convex spaces. Note that the well-known Hilbert spaces are special cases of Banach spaces. The more formal treatment allows many theorems from ordinary calculus and analysis to be generalized to corresponding theorems in functional analysis, as well as numerous new theorems to be stated.
Using the delta function as a test function
The definition given above is based on a relationship that holds for all test functions f, so one might think that it should hold also when f is chosen to be a specific function as the delta function. However, the latter is not a valid test function.
In the definition, the functional derivative describes how the functional ![F[\varphi(x)]](/2012-wikipedia_en_all_nopic_01_2012/I/5cc6c1a5b62d542e444dd9a4905c5f64.png) changes as a result of a small change in the entire function
changes as a result of a small change in the entire function 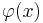 . The particular form of the change in
. The particular form of the change in 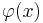 is not specified, but it should stretch over the whole interval on which
is not specified, but it should stretch over the whole interval on which  is defined. Employing the particular form of the perturbation given by the delta function has the meaning that
is defined. Employing the particular form of the perturbation given by the delta function has the meaning that 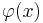 is varied only in the point
is varied only in the point  . Except for this point, there is no variation in
. Except for this point, there is no variation in 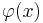 .
.
Often a physicist wants to know how one quantity, say the electric potential  at position
at position 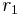 , is affected by changing another quantity, say the density of electric charge
, is affected by changing another quantity, say the density of electric charge  at position
at position 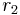 . The potential at a given position is a functional of the density, that is, given a particular density function and a point in space, one can compute a number which represents the potential of that point in space due to the specified density function. Since we are interested in how this number varies across all points in space, we treat the potential as a function of
. The potential at a given position is a functional of the density, that is, given a particular density function and a point in space, one can compute a number which represents the potential of that point in space due to the specified density function. Since we are interested in how this number varies across all points in space, we treat the potential as a function of  . To wit,
. To wit,
That is, for each  , the potential
, the potential 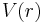 is a functional of
is a functional of 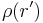 . Applying the definition of functional derivative,
. Applying the definition of functional derivative,
So,
Now we can evaluate the functional derivative at 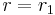 and
and 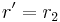 to see how the potential at
to see how the potential at 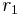 is changed due to a small variation in the density at
is changed due to a small variation in the density at 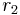 , but in general the unevaluated form is probably more useful.
, but in general the unevaluated form is probably more useful.
Examples
We give a formula to derive a common class of functionals that can be written as the integral of a function and its derivatives. This is a generalization of the Euler–Lagrange equation: indeed, the functional derivative was introduced in physics within the derivation of the Lagrange equation of the second kind from the principle of least action in Lagrangian mechanics (18th century). The first three examples below are taken from density functional theory (20th century), the fourth from statistical mechanics (19th century).
Formula for the integral of a function and its derivatives
Given a functional of the form
with  vanishing at the boundaries of
vanishing at the boundaries of 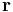 , the scalar product of the functional derivative with a function
, the scalar product of the functional derivative with a function  can be written
can be written
where, in the third line, 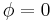 is assumed at the integration boundaries. Thus the functional derivative is
is assumed at the integration boundaries. Thus the functional derivative is
or, writing the expression more explicitly,
The above example is specific to the particular case that the functional depends on the function 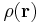 and its gradient
and its gradient 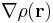 only. In the more general case that the functional depends on higher order derivatives, i.e.
only. In the more general case that the functional depends on higher order derivatives, i.e.
where 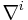 is a tensor whose
is a tensor whose 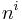 components
components 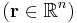 are all partial derivative operators of order
are all partial derivative operators of order  , i.e.
, i.e. 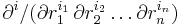 with
with  , an analogous application of the definition yields
, an analogous application of the definition yields
Thomas-Fermi kinetic energy functional
The Thomas-Fermi model of 1927 used a kinetic energy functional for a noninteracting uniform electron gas in a first attempt of density-functional theory of electronic structure:
![T_\mathrm{TF}[\rho]](/2012-wikipedia_en_all_nopic_01_2012/I/5d678034ecc0ff52a5f4f89b09037d2a.png) depends only on the charge density
depends only on the charge density 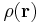 and does not depend on its gradient, Laplacian, or other higher-order derivatives (functionals like this are called “local”). Therefore,
and does not depend on its gradient, Laplacian, or other higher-order derivatives (functionals like this are called “local”). Therefore,
Coulomb potential energy functional
For the classical part of the potential, Thomas and Fermi employed the Coulomb potential energy functional
Again, ![J[\rho]](/2012-wikipedia_en_all_nopic_01_2012/I/b482af29c7386976956a96e9da5ddcff.png) depends only on the charge density
depends only on the charge density  and does not depend on its gradient, Laplacian, or other higher-order derivatives (i.e., it is a “local” functional). Therefore,
and does not depend on its gradient, Laplacian, or other higher-order derivatives (i.e., it is a “local” functional). Therefore,
The second functional derivative of the Coulomb potential energy functional is
Weizsäcker kinetic energy functional
In 1935 von Weizsäcker proposed to add a gradient correction to the Thomas-Fermi kinetic energy functional to make it suit better a molecular electron cloud:
Now ![T_\mathrm{W}[\rho]](/2012-wikipedia_en_all_nopic_01_2012/I/2ebbf901d37d3167a5c46df702220f61.png) depends on the charge density
depends on the charge density  and its gradient
and its gradient 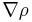 , therefore
, therefore
Writing a function as a functional
Finally, note that any function can be written in terms of an integral functional. For example,
This functional depends on  only, as the first two examples above (i.e., they are all “local”). Therefore,
only, as the first two examples above (i.e., they are all “local”). Therefore,
Entropy
The entropy of a discrete random variable is a functional of the probability mass function.
Thus,
Thus,
Exponential
Let
Using the delta function as a test function,
Thus,
References
- R. G. Parr, W. Yang, “Density-Functional Theory of Atoms and Molecules”, Oxford University Press, Oxford 1989.
- B. A. Frigyik, S. Srivastava and M. R. Gupta, Introduction to Functional Derivatives, UWEE Tech Report 2008-0001. http://www.ee.washington.edu/research/guptalab/publications/functionalDerivativesIntroduction.pdf
![\left\langle \frac{\delta F[\varphi(x)]}{\delta\varphi(x)}, f(x) \right\rangle = \int \frac{\delta F[\varphi(x)]}{\delta\varphi(x')} f(x')dx' = \lim_{\varepsilon\to 0}\frac{F[\varphi(x)%2B\varepsilon f(x)]-F[\varphi(x)]}{\varepsilon} = \left.\frac{d}{d\epsilon}F[\varphi%2B\epsilon f]\right|_{\epsilon=0}.](/2012-wikipedia_en_all_nopic_01_2012/I/60b5b5bbfec50e4ba715215c24c239af.png)
![\frac{\delta F[\varphi(x)]}{\delta \varphi(y)}=\lim_{\varepsilon\to 0}\frac{F[\varphi(x)%2B\varepsilon\delta(x-y)]-F[\varphi(x)]}{\varepsilon}.](/2012-wikipedia_en_all_nopic_01_2012/I/2fbd20c9c47cad7cd0f2ff4147891146.png)
![V(r) = F[\rho] = \frac{1}{4\pi\epsilon_0} \int \frac{\rho(r')}{|r-r'|} \mathrm{d}r'.](/2012-wikipedia_en_all_nopic_01_2012/I/12f3b0d1a58454fcd5b40580376870fa.png)
![\begin{align}
\left\langle \frac{\delta F[\rho]}{\delta \rho(r')}, f(r') \right\rangle
& {} = \frac{d}{d\varepsilon} \left. \frac{1}{4\pi\epsilon_0} \int \frac{\rho(r') %2B \varepsilon f(r')}{|r-r'|} \mathrm{d}r' \right|_{\varepsilon=0} \\
& {} = \frac{1}{4\pi\epsilon_0} \int \frac{f(r')}{|r-r'|} \mathrm{d}r' \\
& {} = \left\langle \frac{1}{4\pi\epsilon_0|r-r'|}, f(r') \right\rangle.
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/0de2b7465bb3b9545656bc0a0f914bd5.png)
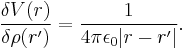
![F[\rho(\mathbf{r})] = \int f( \mathbf{r}, \rho(\mathbf{r}), \nabla\rho(\mathbf{r}) )\, d\mathbf{r},](/2012-wikipedia_en_all_nopic_01_2012/I/8c026b789e0e196729faa20b80024717.png)
![\begin{align}
\left\langle \frac{\delta F[\rho]}{\delta\rho}, \phi \right\rangle
& {} = \frac{d}{d\varepsilon} \left. \int f( \mathbf{r}, \rho %2B \varepsilon \phi, \nabla\rho%2B\varepsilon\nabla\phi )\, d\mathbf{r} \right|_{\varepsilon=0} \\
& {} = \int \left( \frac{\partial f}{\partial\rho} \phi %2B \frac{\partial f}{\partial\nabla\rho} \cdot \nabla\phi \right) d\mathbf{r} \\
& {} = \int \left[ \frac{\partial f}{\partial\rho} \phi %2B \nabla \cdot \left( \frac{\partial f}{\partial\nabla\rho} \phi \right) - \left( \nabla \cdot \frac{\partial f}{\partial\nabla\rho} \right) \phi \right] d\mathbf{r} \\
& {} = \int \left[ \frac{\partial f}{\partial\rho} \phi - \left( \nabla \cdot \frac{\partial f}{\partial\nabla\rho} \right) \phi \right] d\mathbf{r} \\
& {} = \left\langle \frac{\partial f}{\partial\rho} - \nabla \cdot \frac{\partial f}{\partial\nabla\rho}\,, \phi \right\rangle,
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/34e4d3b78625fcd04d717192d14f1a25.png)
![\frac{\delta F[\rho]}{\delta\rho} = \frac{\partial f}{\partial\rho} - \nabla \cdot \frac{\partial f}{\partial\nabla\rho}](/2012-wikipedia_en_all_nopic_01_2012/I/7ba85aee1eb91f707e7989d2cdcb1c0d.png)
![\frac{\delta F[\rho(\mathbf{r})]}{\delta\rho(\mathbf{r})} = \frac{\partial}{\partial\rho(\mathbf{r})}f(\mathbf{r}, \rho(\mathbf{r}), \nabla\rho(\mathbf{r})) - \nabla \cdot \frac{\partial}{\partial\nabla\rho(\mathbf{r})}f(\mathbf{r}, \rho(\mathbf{r}), \nabla\rho(\mathbf{r}))](/2012-wikipedia_en_all_nopic_01_2012/I/a86768022f4b9ce288d05202a0049e21.png)
![F[\rho(\mathbf{r})] = \int f( \mathbf{r}, \rho(\mathbf{r}), \nabla\rho(\mathbf{r}), \nabla^2\rho(\mathbf{r}), \dots, \nabla^N\rho(\mathbf{r}))\, d\mathbf{r},](/2012-wikipedia_en_all_nopic_01_2012/I/10b3b5e43d14217796295cc121b6bc33.png)
![\begin{align}
\frac{\delta F[\rho]}{\delta \rho} &{} = \frac{\partial f}{\partial\rho} - \nabla \cdot \frac{\partial f}{\partial(\nabla\rho)} %2B \nabla^2 \cdot \frac{\partial f}{\partial\left(\nabla^2\rho\right)} %2B \dots %2B (-1)^N \nabla^N \cdot \frac{\partial f}{\partial\left(\nabla^N\rho\right)} \\
&{} = \sum_{i=0}^N (-1)^{i}\nabla^i \cdot \frac{\partial f}{\partial\left(\nabla^i\rho\right)}.
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/0cbf6fb8a9df6e78ac4de347803dbb2f.png)
![T_\mathrm{TF}[\rho] = C_\mathrm{F} \int \rho^{5/3}(\mathbf{r}) \, d\mathbf{r}.](/2012-wikipedia_en_all_nopic_01_2012/I/1128d8968305639a443de81753af2a80.png)
![\frac{\delta T_\mathrm{TF}[\rho]}{\delta \rho} = C_\mathrm{F} \frac{\partial \rho^{5/3}(\mathbf{r})}{\partial \rho(\mathbf{r})} = \frac{5}{3} C_\mathrm{F} \rho^{2/3}(\mathbf{r}).](/2012-wikipedia_en_all_nopic_01_2012/I/c23949e3734c48f9956d2dd27a6655af.png)
![J[\rho] = \frac{1}{2}\iint \frac{\rho(\mathbf{r}) \rho(\mathbf{r}')}{\vert \mathbf{r}-\mathbf{r}' \vert}\, d\mathbf{r} d\mathbf{r}' = \int \left(\frac{1}{2}\int \frac{\rho(\mathbf{r}) \rho(\mathbf{r}')}{\vert \mathbf{r}-\mathbf{r}' \vert} d\mathbf{r}'\right) d\mathbf{r} = \int j[\mathbf{r},\rho(\mathbf{r})]\, d\mathbf{r}.](/2012-wikipedia_en_all_nopic_01_2012/I/1a921152fec0e4e5d29306a42ab19847.png)
![\frac{\delta J[\rho]}{\delta \rho(\mathbf{r})} = \frac{\partial j}{\partial \rho(\mathbf{r})} = \frac{1}{2}\int \frac{\partial}{\partial \rho(\mathbf{r})}\frac{\rho(\mathbf{r}) \rho(\mathbf{r}')}{\vert \mathbf{r}-\mathbf{r}' \vert}\, d\mathbf{r}' = \int \frac{\rho(\mathbf{r}')}{\vert \mathbf{r}-\mathbf{r}' \vert}\, d\mathbf{r}'](/2012-wikipedia_en_all_nopic_01_2012/I/1f185fc46e57aeb54f4b5087713b5a33.png)
![\frac{\delta^2 J[\rho]}{\delta \rho(\mathbf{r}')\delta\rho(\mathbf{r})} = \frac{\partial}{\partial \rho(\mathbf{r}')} \frac{\rho(\mathbf{r}')}{\vert \mathbf{r}-\mathbf{r}' \vert} = \frac{1}{\vert \mathbf{r}-\mathbf{r}' \vert}.](/2012-wikipedia_en_all_nopic_01_2012/I/404c7f2b9080ac0b483be72676f830bc.png)
![T_\mathrm{W}[\rho] = \frac{1}{8} \int \frac{\nabla\rho(\mathbf{r}) \cdot \nabla\rho(\mathbf{r})}{ \rho(\mathbf{r}) } d\mathbf{r} = \frac{1}{8} \int \frac{(\nabla\rho(\mathbf{r}))^2}{\rho(\mathbf{r})}\, d\mathbf{r} = \int t[\rho(\mathbf{r}),\nabla\rho(\mathbf{r})] d\mathbf{r}.](/2012-wikipedia_en_all_nopic_01_2012/I/949c854f6f411ad7887df94f00b5071c.png)
![\frac{\delta T_\mathrm{W}[\rho]}{\delta \rho} = \frac{\partial t}{\partial \rho} - \nabla\cdot\frac{\partial t}{\partial (\nabla \rho)} = -\frac{1}{8}\frac{(\nabla\rho(\mathbf{r}))^2}{\rho(\mathbf{r})^2} - \nabla\cdot\left(\frac{1}{4}\frac{\nabla\rho(\mathbf{r})}{\rho(\mathbf{r})}\right) = \frac{1}{8} \frac{(\nabla\rho(\mathbf{r}))^2}{\rho(\mathbf{r})^2} - \frac{1}{4}\frac{\nabla^2\rho(\mathbf{r})}{\rho(\mathbf{r})}.](/2012-wikipedia_en_all_nopic_01_2012/I/ba83247b284730a0b92ff85634342c92.png)
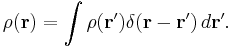
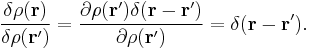
![\begin{align}
H[p(x)] = -\sum_x p(x) \log p(x)
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/cf53c97dc0e3cc75331436114189827a.png)
![\begin{align}
\left\langle \frac{\delta H}{\delta p}, \phi \right\rangle
& {} = \sum_x \frac{\delta H[p(x)]}{\delta p(x')} \, \phi(x') \\
& {} = \left. \frac{d}{d\epsilon} H[p(x) %2B \epsilon\phi(x)] \right|_{\epsilon=0}\\
& {} = -\frac{d}{d\varepsilon} \left. \sum_x [p(x) %2B \varepsilon\phi(x)] \log [p(x) %2B \varepsilon\phi(x)] \right|_{\varepsilon=0} \\
& {} = \displaystyle -\sum_x [1%2B\log p(x)]\phi(x)\\
& {} = \left\langle -[1%2B\log p(x)], \phi \right\rangle.
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/063cb8ddd75e8a0040e4db2adda738c2.png)
![\frac{\delta H}{\delta p} = -[1%2B\log p(x)].](/2012-wikipedia_en_all_nopic_01_2012/I/fe42ea0e4acb036de4e5fff6536b1a08.png)
![F[\varphi(x)]= e^{\int \varphi(x) g(x)dx}.](/2012-wikipedia_en_all_nopic_01_2012/I/ccd161f924f4826e0c0d450523fd1c8b.png)
![\begin{align}
\frac{\delta F[\varphi(x)]}{\delta \varphi(y)}
& {} = \lim_{\varepsilon\to 0}\frac{F[\varphi(x)%2B\varepsilon\delta(x-y)]-F[\varphi(x)]}{\varepsilon}\\
& {} = \lim_{\varepsilon\to 0}\frac{e^{\int (\varphi(x)%2B\varepsilon\delta(x-y)) g(x)dx}-e^{\int \varphi(x) g(x)dx}}{\varepsilon}\\
& {} = e^{\int \varphi(x) g(x)dx}\lim_{\varepsilon\to 0}\frac{e^{\varepsilon \int \delta(x-y) g(x)dx}-1}{\varepsilon}\\
& {} = e^{\int \varphi(x) g(x)dx}\lim_{\varepsilon\to 0}\frac{e^{\varepsilon g(y)}-1}{\varepsilon}\\
& {} = e^{\int \varphi(x) g(x)dx}g(y).
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/d2e79ce701a74cf3b196dca84b7c6d2f.png)
![\frac{\delta F[\varphi(x)]}{\delta \varphi(y)} = g(y) F[\varphi(x)].](/2012-wikipedia_en_all_nopic_01_2012/I/80d772725436eb1d9ef32a31a6fa1cd2.png)